速度和速率的区别(举例说明速度与速率之间的联系)
速度和速率是两个不同的概念,它们既有区别,也有联系,很多学生会弄不清它们之间的区别和联系,你知道这是为什么吗?

小学的时候我们就接触到“速度”,然而这个概念却是错误的,很多中小学教师自己也分不清速度和速率的区别,所以当他们说到路程和时间的比值,或者距离和时间的比值时,往往都会告诉学生,这就是速度。
其实错了,这里的正确概念是速率,而不是速度。也有一部分教师其实懂得速度和速率的区别,但是早就习惯张口就“速度”,不太习惯说“速率”,久而久之,学生就只知道速度而不知道速率了。
而且在很多课外练习中,也都有速度代替速率,甚至连教材都有这样的情况。
几乎已经被默认了,中小学的速度就是速率,长此以往,学生又怎么可能区分得清速度和速率呢?印象中,高中也很少把这个问题区分清楚的。
速度和速率都是用来表示物体的运动的快慢的,区别在于速度有方向,而速率没有方向。在数学上,没有方向的量叫做标量,有方向的量叫做矢量或者向量。
速率等于路程和时间的比,或者距离和时间的比,而路程、距离、时间都是标量,它们都是有大小,没有方向的。
当然,某种特殊的情况下,时间也可以有方向,不过在研究运动时,我们都是把它当作没有方向的,即时间是不可逆的。因此速率也是没有方向的。
而速度等于位移和时间的比,因为位移有方向,所以速度也有方向,速度的方向和位移的方向相同。
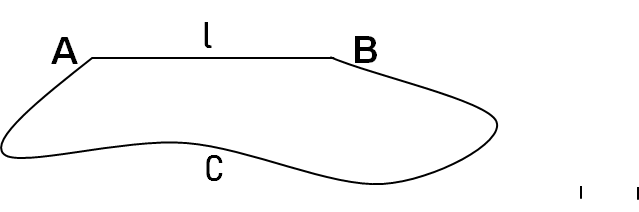
我们举个例子,在A,B间有两条路,一条是线段,记为l,线段长1km;另一条是曲线C,曲线长3。小明在A,B之间运动。
(1)如果小明在C上运动,那么他走过的称为路程,路程=3km. 假如用时3分钟,那么他的速率是1km每分钟。
(2)如果他在l上运动,那么他走过的,可以称为路程,也可以称为距离,距离=1km。假如用时1分钟,那么他的速率也是1km每分钟。
(3)如果他在l上运动,从A到B记为正,从B到A记为负,那么他走过的称为位移,正位移是1km,负位移是-1km. 假如用时还是1分钟,那么他从A到B的速度是1km每分钟,从B到A的速度是-1km每分钟。
可见,在整条曲线中运动只有速率的概念,而在直线中运动,既有速率的概念也有速度的概念。
不过要注意的是,就算在曲线中,瞬时的运动状态也可以有速度的概念,瞬时速度的大小和速率相同,方向在曲线的切线上。
速度就像实数一样,可以把速率看作它的绝对值,但又有所不同,因为有理数只有正负两个方向,而速度的方向却是不确定的,需要指定一条直线,速度的方向才有正负之分。