等腰三角形斜边怎么算（计算等腰三角形斜边的方法）
6983
摘要：等腰三角形是指两个底角的角度相等，底边长度相等的三角形。计算等腰三角形的斜边时，需要使用正弦、余弦和正切等三角函数，通过已知的底角一半的弧度和底边长度来计算斜边长度。需要注意，计算时需将角度转换为弧度制，计算器不但可以计算三角函数的值，还可以帮助我们转换角度制和弧度制。
什么是等腰三角形
等腰三角形是指两个底角（即底边两旁的角）的角度相等的三角形，底边的长度也相等。简单来说，就是有两条边相等的三角形。
如何计算等腰三角形斜边
在计算等腰三角形的斜边时，我们需要使用三角函数，包括正弦、余弦和正切。这些三角函数中的每一个都与一个角度有关，我们需要知道角度的大小以及另外两条边的长度才能计算出斜边的长度。
我们可以通过以下公式来计算等腰三角形的斜边：
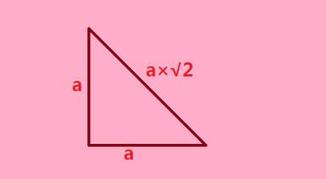
斜边 = 底边 ÷ 正（底角的一半）
其中，底边指的是等腰三角形的两条底边中的任意一条，底角指的是底边两旁的角，因为等腰三角形的两个底角是相等的，所以计算斜边只需要用其中一个底角的一半就可以了。
比如，如果等腰三角形的底边AB长度为10，底角CAB的度数为30度，那么我们可以使用下面的公式来计算斜边：
斜边 = 10 ÷ 正（30 ÷ 2）
我们可以使用计算器来计算正弦、余弦和正切函数的值，再将计算结果代入公式中，最终得到斜边的长度。在计算时，需要将角度值转换为弧度制，因为计算机只能处理弧度制。转换角度值为弧度值的公式是：
弧度值 = 角度值 × π ÷ 180
其中，π是一个常数，约等于3.14159。
实例
假设等腰三角形的底边长为6，顶角的度数为60度，那么我们可以使用以下公式来计算斜边：
弧度制的60度 = 60 × π ÷ 180 = 1.0472
斜边 = 6 ÷ 正（60 ÷ 2） = 6 ÷ 正（30） = 6 ÷ 0.5 = 12
因此，这个等腰三角形的斜边长为12。
结论
等腰三角形是指两个底角的角度相等，底边长度相等的三角形。计算等腰三角形的斜边时，需要使用正弦、余弦和正切等三角函数，通过已知的底角一半的弧度和底边长度来计算斜边长度。
需要注意，计算时需将角度转换为弧度制，计算器不但可以计算三角函数的值，还可以帮助我们转换角度制和弧度制。
