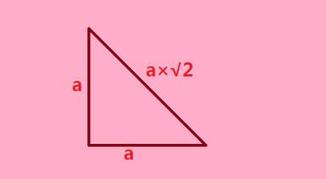
三角形边长算(如何计算三角形的边长)
三角形的基本概念
三角形是平面几何图形中最基本的形状之一,由三个线段连接而成,其中包含三个内角和三条边。在三角形中,每个角度总和为180度。
三角形的边界为其三个边与其角度之间所形成的线段,其中其中一个边被称为“底边”,其他两个边分别被称为“腰”。
如何计算三角形的边长
在计算三角形边长时,最简单的方法是通过先确定一个角度、旁边一个边或旁边的两条边来确定其余的边。以下是各种不同情况下计算三角形边长的方法。
情况一:提供三角形的三个角度
如果已知三角形的三个角度,则可以通过以下公式轻松计算其边长。
假设三角形的三个角度分别为A、B和C,则三角形每个角度的大小可以用以下公式来计算:
A = cos-1[(b2 + c2 - a2)/2bc]
B = cos-1[(a2 + c2 - b2)/2ac]
C = cos-1[(a2 + b2 - c2)/2ab]
在这些公式中,a,b和c分别代表三角形的三边。
通过三个既定的角度,可以使用这些公式确定三角形的三条边长。
情况二:提供一个角度和旁边一个边
如果已知三角形的一个角度和旁边一个边,则可以使用以下公式计算其余的两个边长。
假设一个角度为A,与其相邻的边长度为b,其他两个边分别为a和c,则可以使用以下公式计算其余两个边的长度:
a = b/sinA
c = b/sinC
在这些公式中,sin表示正弦函数,A和C分别表示与b相邻的角度。
情况三:提供两个角度和与其相邻的边
如果已知三角形的两个角度和与其相邻的一个边,则可以使用以下公式计算其余两个边长。
假设两个角度分别为A和B,与B相邻的边的长度为b,其他两个边长度为a和c,则可以使用以下公式计算其余两个边的长度:
a = (b x sinA)/sinB
c = (b x sinC)/sinB
在这些公式中,sin表示正弦函数,A和C分别表示与b相反的角度。
总结
三角形的边长计算是解决数学问题的重要一环。有了正确的公式和方法,可以轻松确定三角形的各个要素,从而计算出其余的元素。因此,在处理与三角形相关的问题时,理解这些方法非常重要。